In construction and civil engineering & any other areas, we often deal with irregular shapes while preparing drawings or taking site measurements etc. One such common case is when a rectangular area is trimmed by a diagonal cut, creating a slanted side.
In this article, we will find it out how to calculate the slanted side of the figure shown the image
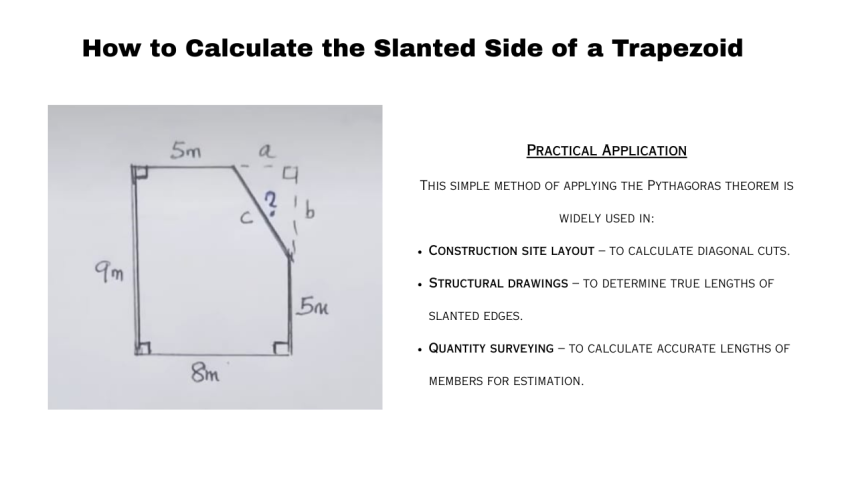
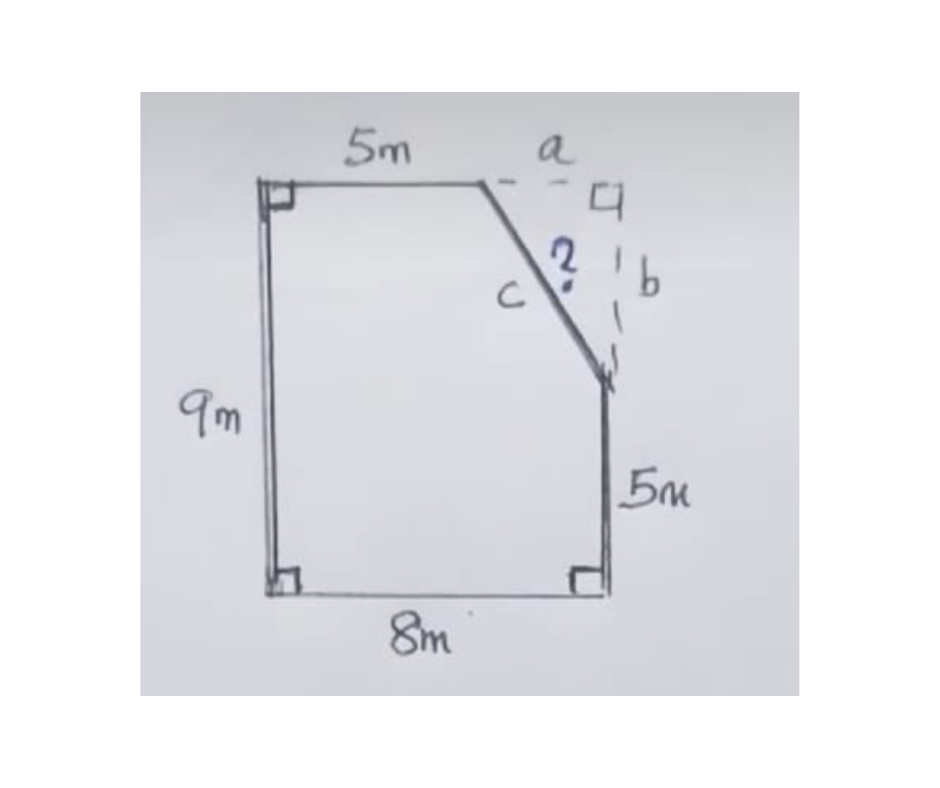
Given Dimensions From the image
- Left vertical side = 9 m
- Bottom horizontal side = 8 m
- Top horizontal side = 5 m
- Right vertical side (below chamfer) = 5 m
- Slanted side = c (to be calculated)
The figure can be visualized as a rectangle where the top-right corner is cut off by a diagonal line.
Step 1: Identify the right-angled triangle
From the image:
Bottom Horizontal length is 8m & Top Horizontal length is 5m
So, a = 8 – 5 = 3 m
Left Vertical side is 9m & Right Vertical Side is 5m
So. b = 9 -5 = 4m
This forms a right-angled triangle with:
- a = 3m
- b = 4m
- Hypotenuse = c (the slanted side we need).
Step 2: Apply Pythagoras Theorem
The Pythagoras theorem states:
a² + b² = c²
3² + 4² = c² , c² = 9+ 16 ,
c² = 25, c = √25
c = 5 m, The length of the slanted side is: c = 5m
Practical Application
This simple method of applying the Pythagoras theorem is widely used in:
- Construction site layout – to calculate diagonal cuts.
- Structural drawings – to determine true lengths of slanted edges.
- Quantity surveying – to calculate accurate lengths of members for estimation.